Các dạng toán liên quan đến phương trình tiếp tuyến – Diệp Tuân
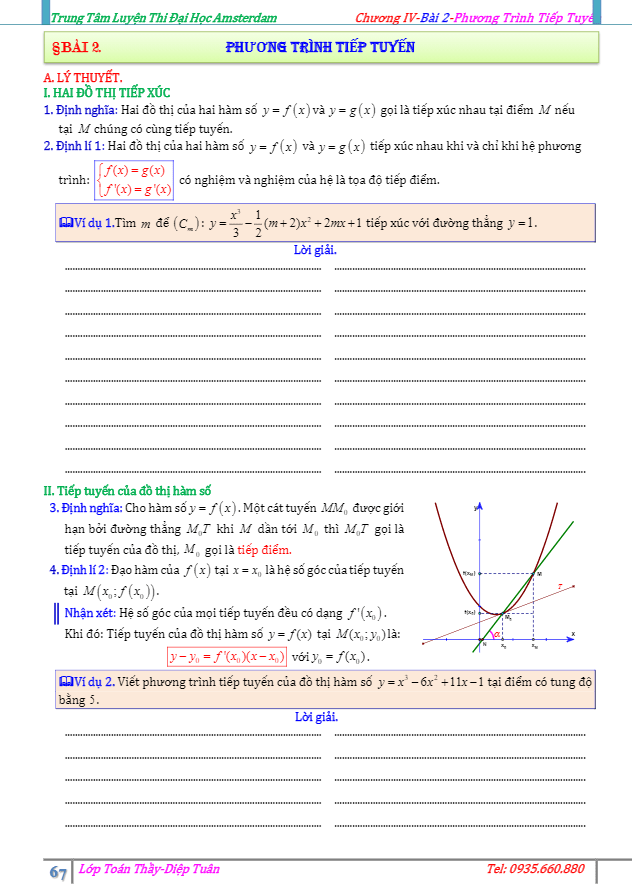
Trong toán học, phương trình tiếp tuyến là một phương trình đại số mô tả mối quan hệ giữa hàm số và đường tiếp tuyến tại một điểm trên đồ thị của hàm số đó. Các dạng toán liên quan đến phương trình tiếp tuyến thường được áp dụng để giải các bài toán về đạo hàm và các ứng dụng trong thực tế.
Một trong những dạng toán phổ biến liên quan đến phương trình tiếp tuyến là tính độ dốc của đường tiếp tuyến tại một điểm trên đồ thị của hàm số. Để tính được độ dốc này, ta cần sử dụng đạo hàm của hàm số tại điểm đó. Phương trình của đường tiếp tuyến tại điểm đó có thể được xác định thông qua độ dốc và tọa độ của điểm đó.
Ngoài ra, còn có dạng toán liên quan đến việc tìm điểm cắt giữa đường tiếp tuyến và các đường cong khác trên đồ thị của hàm số. Điều này đòi hỏi việc giải hệ phương trình giữa phương trình tiếp tuyến và phương trình của đường cong đó để xác định tọa độ của điểm cắt.
Diệp Tuân, một chuyên gia về đạo hàm và các ứng dụng của nó, đã nghiên cứu và áp dụng các dạng toán liên quan đến phương trình tiếp tuyến vào nhiều lĩnh vực khác nhau. Nhờ vào kiến thức sâu rộng và kinh nghiệm thực tiễn, anh đã đưa ra nhiều phương pháp giải quyết hiệu quả cho các bài toán phức tạp liên quan đến phương trình tiếp tuyến.
Trong tổ hợp các dạng toán này, việc hiểu và áp dụng chính xác các định lý và công thức liên quan đến phương trình tiếp tuyến là rất quan trọng. Đồng thời, kỹ năng suy luận và giải quyết vấn đề cũng đóng vai trò quan trọng trong việc giải các bài toán này một cách chính xác và nhanh chóng.