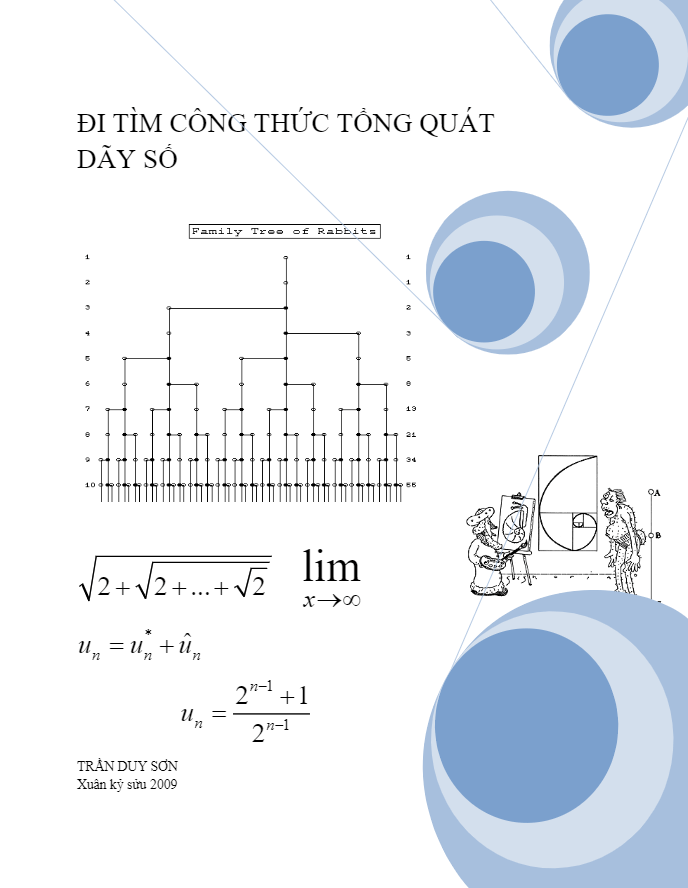
Đi tìm công thức tổng quát của dãy số – Trần Duy Sơn
Trong toán học, việc tìm công thức tổng quát của một dãy số là một vấn đề quan trọng và hữu ích. Trần Duy Sơn, một chuyên gia trong lĩnh vực này, đã đưa ra phương pháp giúp giải quyết vấn đề này một cách hiệu quả.
Theo Trần Duy Sơn, để tìm công thức tổng quát của một dãy số cấp số cộng, ta cần biết hai thông số chính là số hạng đầu tiên của dãy (a) và công sai giữa hai số hạng liên tiếp (d). Công thức tổng quát của dãy số cấp số cộng có dạng:
S(n) = n/2 * [2a + (n-1)d]
Trong đó, S(n) là tổng của n số hạng đầu tiên của dãy, a là số hạng đầu tiên, d là công sai giữa hai số hạng liên tiếp, và n là số lượng số hạng cần tính tổng.
Đối với dãy số cấp số nhân, công thức tổng quát có dạng:
S(n) = a * (1 - r^n) / (1 - r)
Trong đó, S(n) là tổng của n số hạng đầu tiên của dãy, a là số hạng đầu tiên, r là công bội giữa hai số hạng liên tiếp, và n là số lượng số hạng cần tính tổng.
Nhờ vào công thức này, việc tính toán tổng của các dãy số cấp số cộng và cấp số nhân trở nên đơn giản và nhanh chóng. Trần Duy Sơn đã đem lại những kiến thức hữu ích và tiện lợi cho cộng đồng toán học.